跳转至

Block Cipher Modes of Operation

约 1585 个字 14 张图片 预计阅读时间 5 分钟

有几种 使用分组密码构建加密算法 的标准方法(或操作模式):

  • ECB Mode (Electronic Code Book)
  • CBC Mode (Cipher Block Chaining)
  • Counter (CTR) Mode
  • CFB Mode (Ciphertext Feedback Mode)
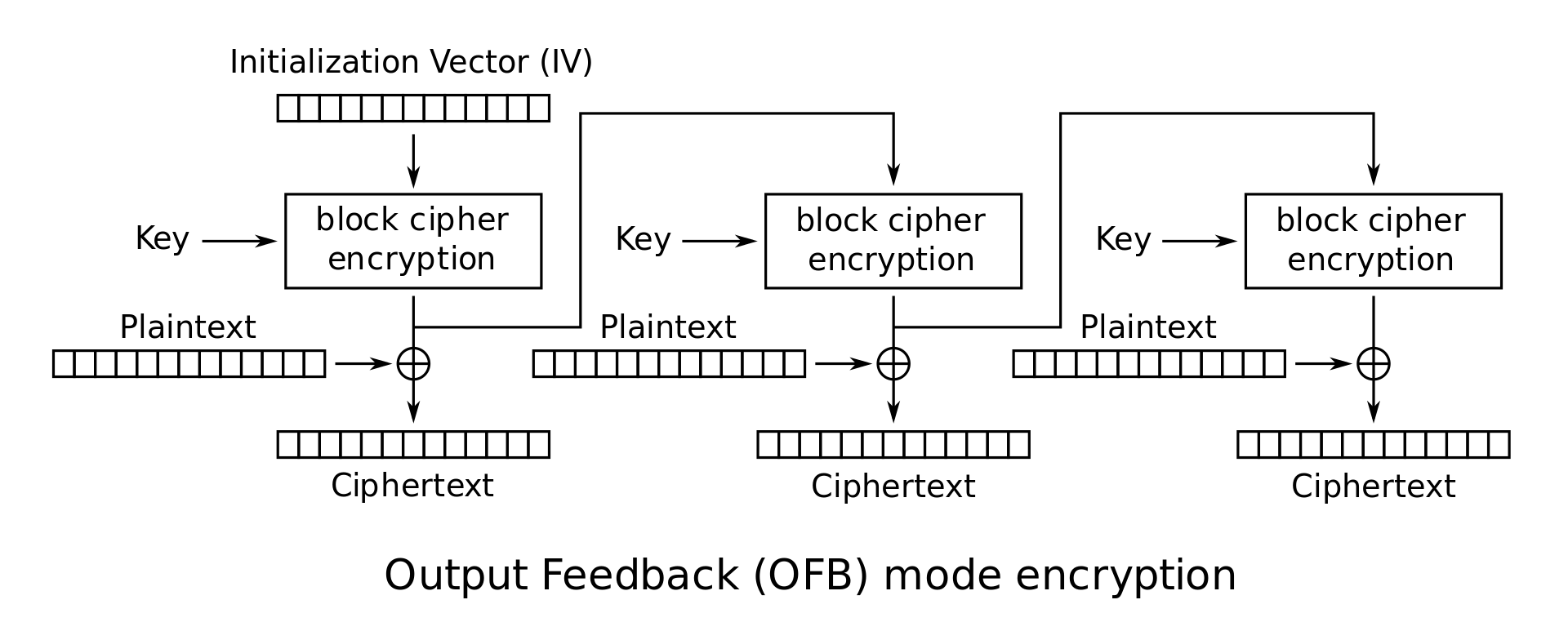
  • OFB Mode (Output Feedback Mode)

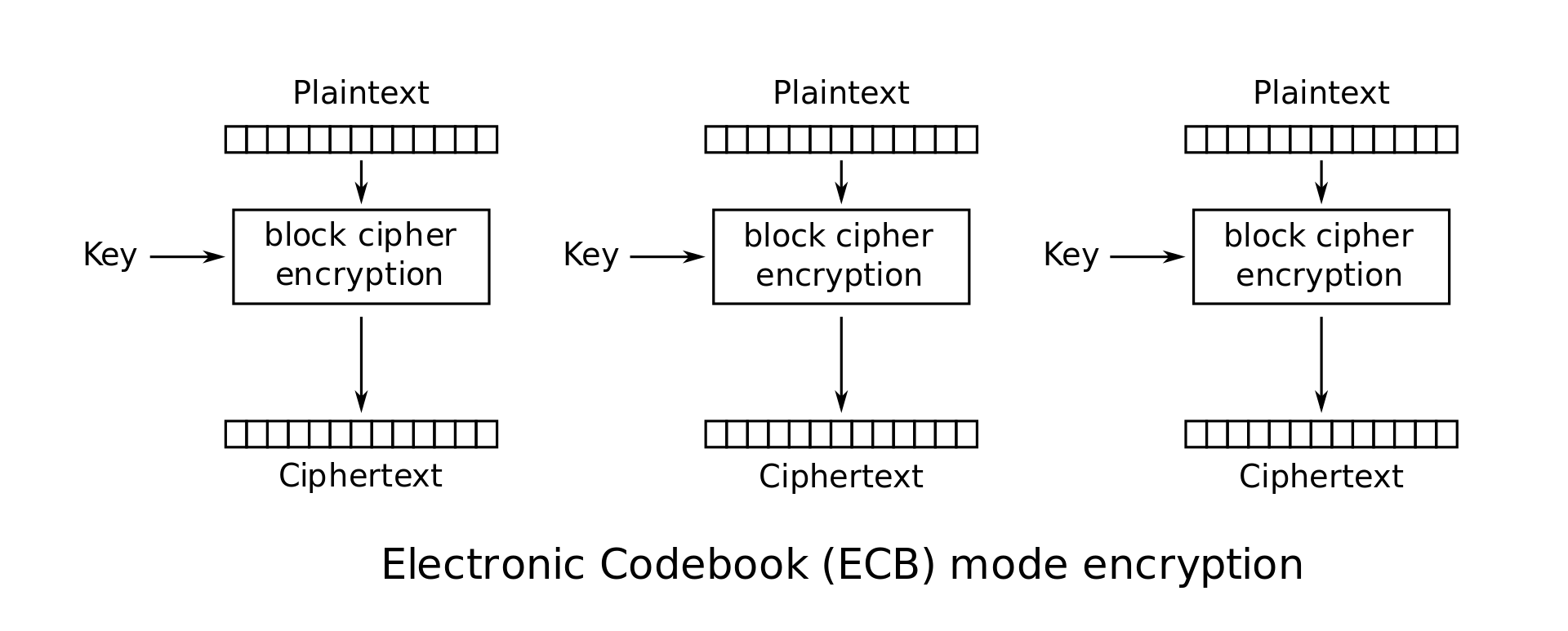
ECB

假设AES现在只能加密128bit的消息，那么如何加密更长的？(比如256bit)

  • Idea： 使用AES更多次（比如若256bit，则用两次）

在这种模式中，明文M被分为n-bit的块\(M_1...M_m\)(假设m是M中明文块的数量，每个块的大小为n)，并且每个利用分组密码进行 加密: \(C_i = E_K(M_i)\)，密文只是这些单独块的连接: \(C = C_1 \cdot C_2 \cdots C_m\)，因ECB是确定的，故AES-ECB不是AND-CPA安全

ECB

PS: 解密 → \(M_i = D_K(C_i)\)

缺陷：可能泄露明文的信息。 比如：如果\(M_i = M_j\)，则\(C_i = C_j\)

Example

origin

ECB加密

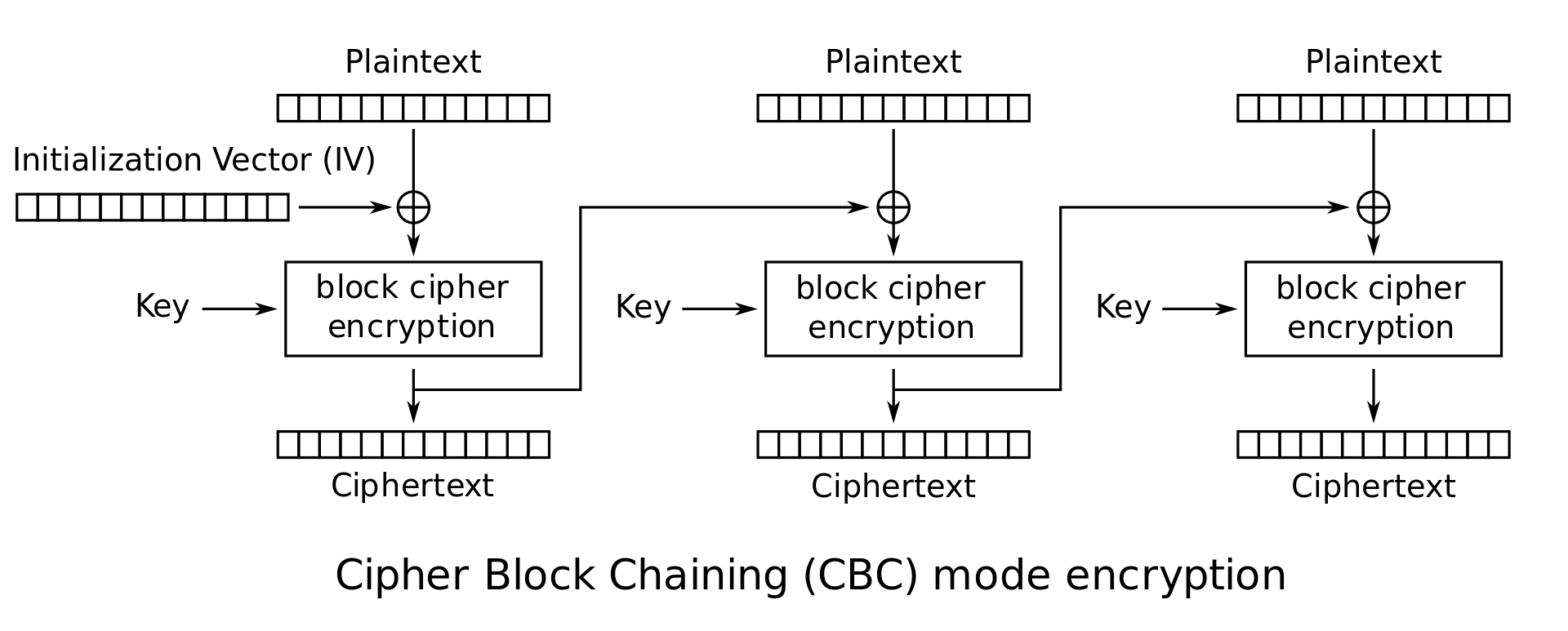
CBC

通过添加一些 随机性 来解决上述问题

给出初始化向量，它对于每种加密都是不同的。此时每个加密的第一个密文块将都是不同的!

此时因第一个密文块的计算具有一定的随机性，之后再给后面的块添加随机性，如图

CBC加密

加密：\(C_0 = IV, C_i = E_K(M_i \bigoplus C_{i - 1})\)

  • 将M拆分为m个明文块\(P_1 \cdots P_m\),每个块大小为n
  • 随机一个随机的IV
  • 计算并输出\((IV, C_1, \cdots, C_m)\)作为整个密文

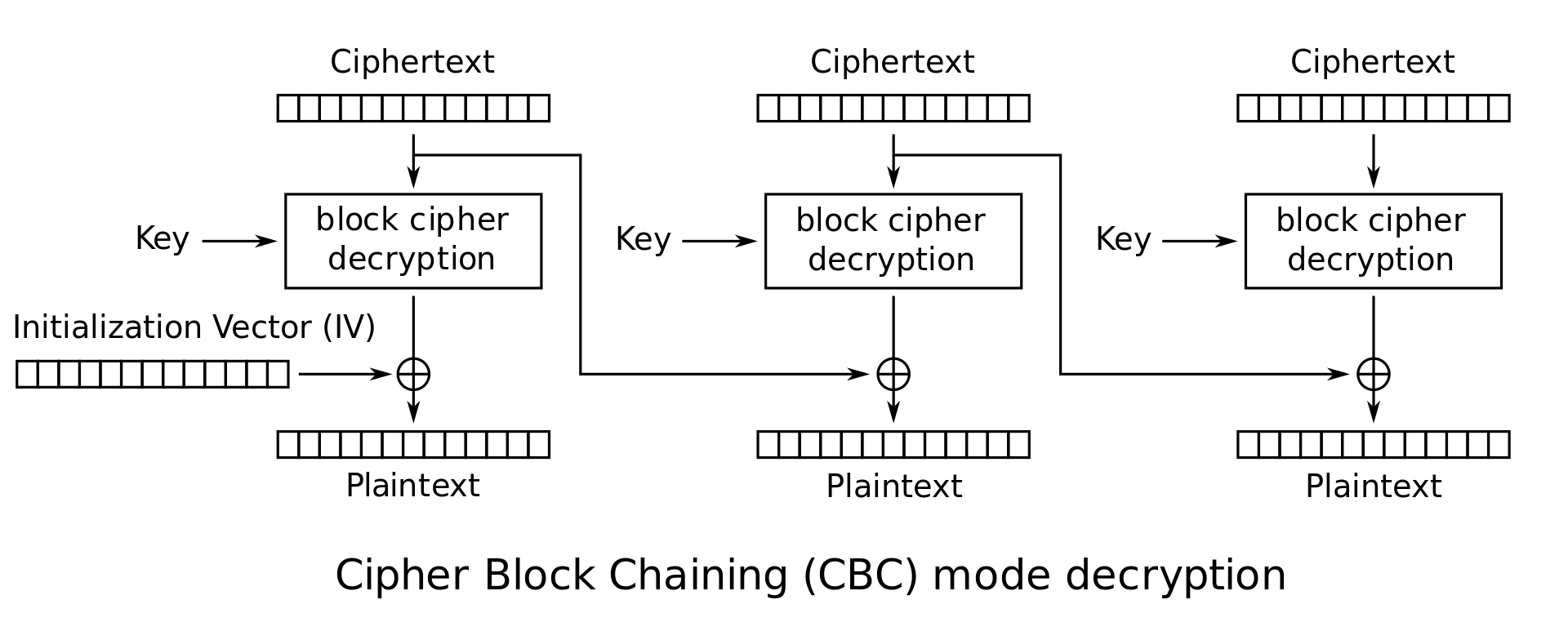
那么如何进行解密？→ 对密文两边先进行解密，再两边进行\(\bigoplus\)操作，如下：

\[ \begin{align} & \because C_i = E_K(M_i \bigoplus C_{i - 1}) \\ & \therefore D_K(C_i) = D_K(E_K(M_i \bigoplus C_{i - 1})) \\ & \therefore D_K(C_i) = M_i \bigoplus C_{i - 1} \\ & \because D_K(C_i) \bigoplus C_{i - 1} = M_i \bigoplus C_{i - 1} \bigoplus C_{i - 1} \\ & \therefore D_K(C_i) \bigoplus C_{i - 1} = M_i \end{align} \]

即 解密 ：\(M_i = D_K(C_i) \bigoplus C_{i - 1}\)

Q: 加密和解密可以并行化吗？

  • 加密：不可以！必须等待区块i完成后才能加密区块i+1
  • 解密：可以！仅仅需要密文作为输入

CBC解密

Q: 如果要加密的消息不是块大小的倍数，该怎么办?

(明文长度是块大小的倍数AES-CBC才可被定义)

解决办法: 填充消息，直到它是块大小的倍数

  • 填充(padding):在消息的末尾添加虚拟字节(dummy bytes)，直到它达到适当的长度

那么应该采取哪种填充的方案？

一个正确的填充方案是PKCS#7，根据所使用的填充字节数填充消息

  • 如果需要1个字节，用01填充;如果需要3个字节，就用03 03 03填充
  • 如果需要0个填充字节，则填充整个虚拟块

如果IV随机生成，并且不重复使用，则AES-CBC是IND-CPA安全的

Example

origin

CBC_IV

CTR

如果我们不重复使用密钥key，one-time pads 就很安全; 如果攻击者不知道密钥，则分组密码的输出看起来就是随机的 → Idea: 可以使用分组密码来模拟 one-time pads 吗?

使用随机输出作为 one-time pad → 记住 one-time pads :将pad与明文进行XOR获得密文

CTR

那么应该用什么作为分组密码的输入?

  • IND-CPA方案需要随机性，所以放置一个随机的nonce
    • PS: 这里的随机值被命名为nonce，其思想与CBC模式中的IV相同
  • counter每个块递增，以确保每个块密码输出是不同的

CTR_encryption

加密Enc(K, M)：

  • 将M拆分为明文块\(P_1…P_m\)(每个块大小为n)
  • 选择随机的nonce
  • 计算和输出\((Nonce, C_1,…,C_m)\)

如何进行解密？ → 回想one-time pads:使用密文进行XOR以获得明文

  • 解析C为\((Nonce, C_1,…,C_m)\)
  • 计算\(P_i\)，通过\(C_i\)与\(E_k\)在nonce和counter作用下的输出之间进行XOR
  • 连接结果明文并输出\(M = P_1…P_m\)

CTR-decryption PS: 我们只使用分组密码加密，而不使用其解密

Q: 加密和解密可否并行化？ → YES!

Q: 是否需要填充信息？ → 不需要，可以把XOR中比信息长的部分剪掉

如果nonce是随机的并且不被再次使用，则AES-CTR是IND-CPA安全的

如果再次使用了会怎么样？→ 相当于在one-time pads中重复使用密钥

  • one-time pads中密钥重用是灾难性的:通常会泄露足够的信息，使攻击者推断出整个明文

IVs and Nonces ：

初始化向量(IV)：一个随机的，但公开的，一次性使用的值，将随机性引入算法

  • 对于CTR，使用nonce(一次使用的数字)，因为值必须是唯一的，而不一定是随机的

不要重复使用IVs :

  • 在某些算法中，IV/nonce重用会泄漏有限的信息(例如CBC)
  • 在某些算法中，IV/nonce重用会导致灾难性故障(例如CTR)

比较 ：

如果需要高性能，哪种模式更好? → CTR，因为可以并行加密和解密

如果担心安全性，哪种模式更好? → CBC

Note

理论上，如果使用得当，CBC和CTR模式同样安全

但如果使用不当(IV/nonce重用)，CBC只会泄露部分信息，而CTR则会灾难性地失败

Other Modes of Operation

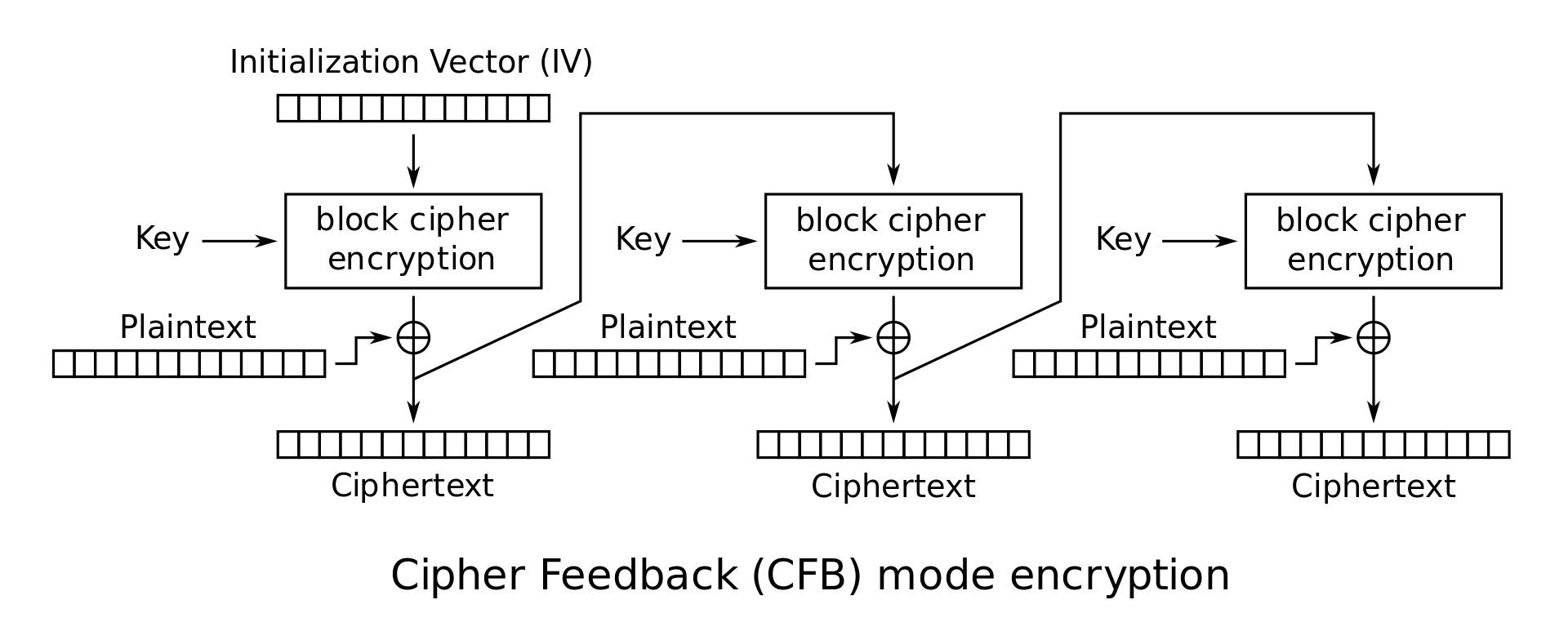
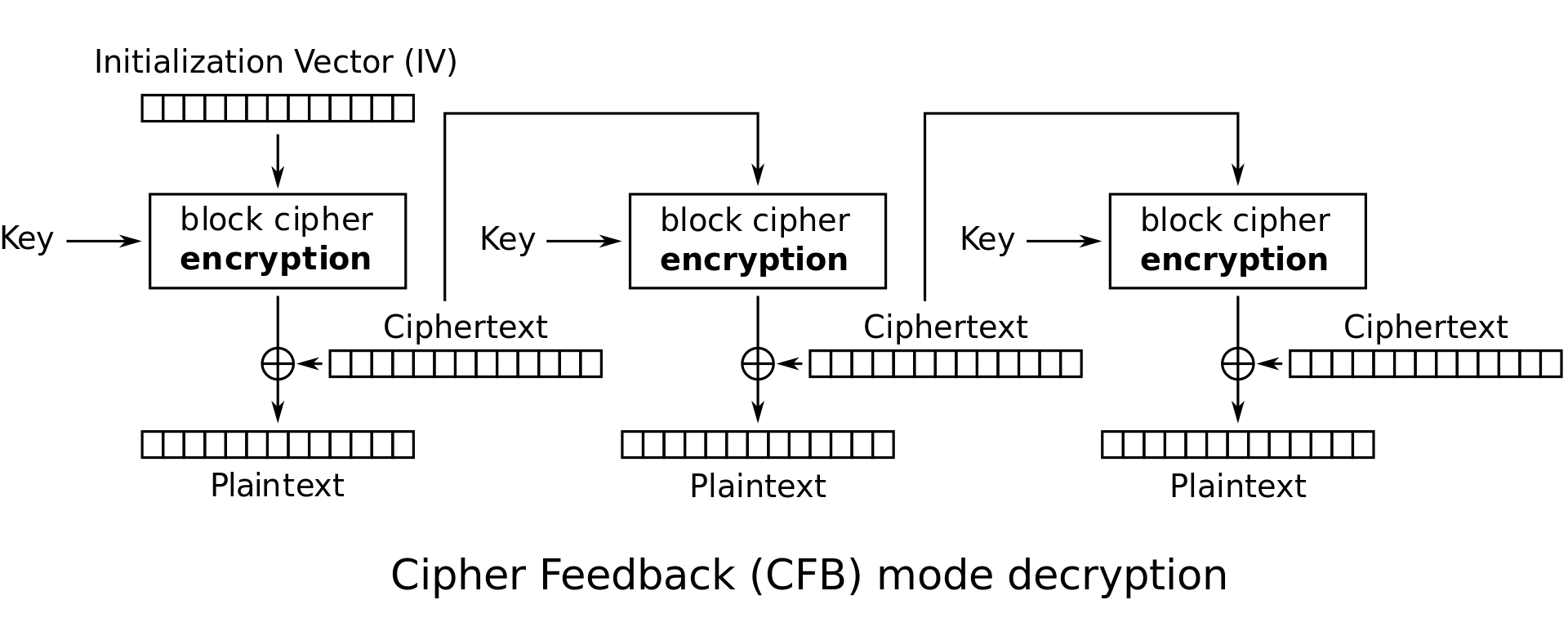
CFB

CFB另一种流行的模式，其属性与CBC模式非常相似。

加密： \(C_0 = IV, C_i = E_K(C_{i - 1}) \bigoplus M_i\)

CFB_encryption

解密: \(M_i = E_K(C_{i - 1}) \bigoplus C_i\)

OFB

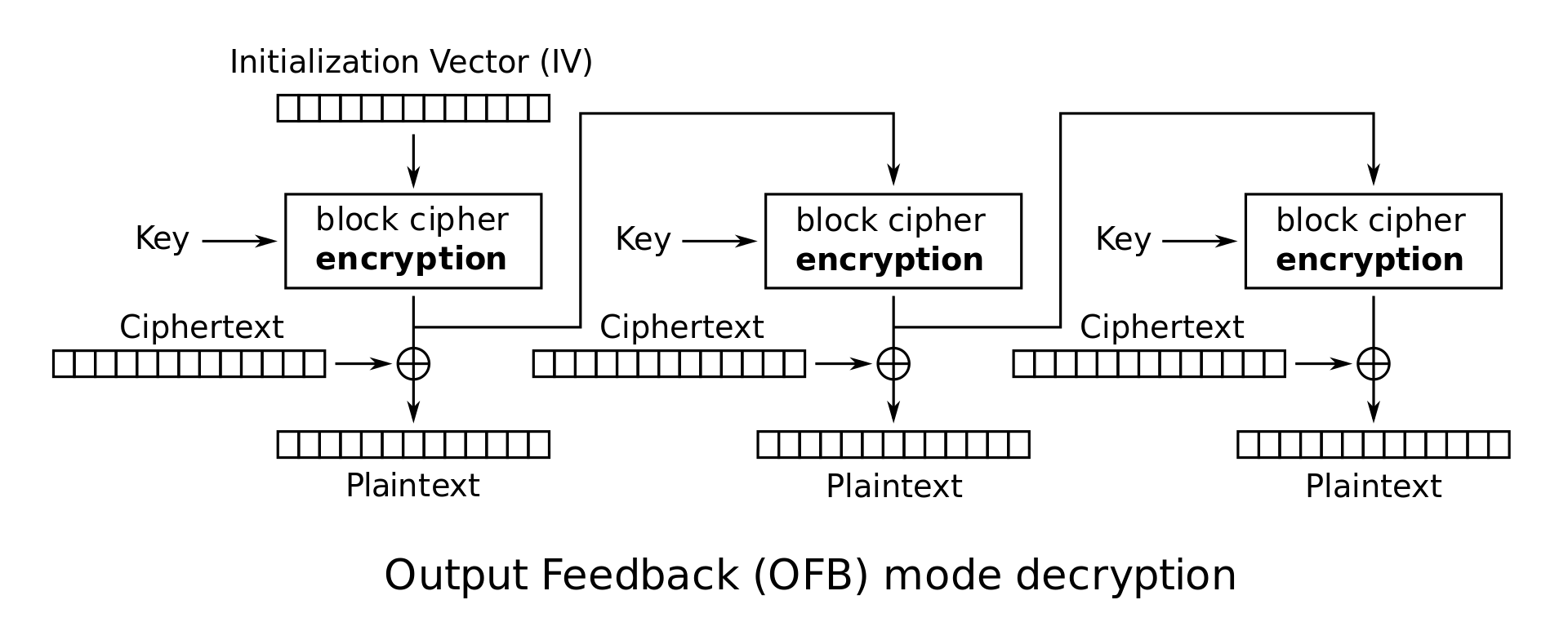
在此模式下，对初始向量IV进行多次加密，得到一组值\(Z_i\)：\(Z_0 = IV, Z_i = E_K(Z_{i - 1})\)，\(Z_i\)被当作one-time pads中的密钥使用，即\(C_i = Z_i \bigoplus M_i\)，也就是密文是初始向量和这些单独块的连接:\(C = IV \cdot C_1 \cdot C_2 \cdots C_m\)

解密： \(M_i = C_i \bigoplus Z_i\)

总述

分组密码是为 保密性(confidentiality) 而设计的(IND-CPA)

但如果攻击者篡改了密文，并不能保证检测到它

还记得Mallory么: 一个想要篡改消息的主动操纵者

即 可能会导致Lack of Integrity(完整性) and Authenticity(真实性)

颜色主题调整

快来和我聊天~

可以的话请给我赞和 star喔~    =>  GitHub stars

评论